Cho một tứ giác ABCD và I là giao điểm của các đường chéo. Chứng minh rằng nếu bán kính các đường tròn nội tiếp các tam giác IAB, IBC, ICD, IDA mà bằng nhau thì ABCD là hình thoi.
Câu hỏi
Nhận biếtCho một tứ giác ABCD và I là giao điểm của các đường chéo. Chứng minh rằng nếu bán kính các đường tròn nội tiếp các tam giác IAB, IBC, ICD, IDA mà bằng nhau thì ABCD là hình thoi.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Trước hết, ta chứng minh bài toán sau đây:
"Cho hai tam giác ABC và AMN với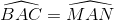 
, các bán kính đường tròn nội tiếp bằng nhau. Chứng minh rằng nếu AB < AM thì AC > AN"
Dựng các tam giác đó như trong hình vẽ sau, trong đó giả sử AC < AN tiếp điểm của BC với đường tròn nội tiếp tam giác ABC là I.
Ta thấy ngay mọi điểm của (O) đều nằm trên nửa mặt phẳng bờ BC có chứa điểm A. Trong đó M, N lần lượt nằm trên các tia đối của tia BA, CA. Suy ra đoạn thẳng MN nằm trên nửa mặt phẳng bờ BC không chứa A, và do đó không có điểm chung với (O) trái với giả thiết và bài toán đã được chứng minh.
Giả sử IA < IC (1), áp dựng bài toán vừa nêu cho ∆ AIB và ∆ CID, ta có: IB > ID hay ID < IB. Lại áp dụng cho tam giác ∆ IAD và ∆ ICB, ta có IA > IC, mâu thuẫn với (1). Vậy IA > IC.
Chứng minh tương tự, ta cũng có IC > IA. Suy ra IA = IC. Một cách tương tự, ta cũng có IB = ID. Vì có cạnh IB chung và IA = IC nên hai tam giác IAB, ICB có diện tích bằng nhau, lại có bán kính đường tròn nội tiếp bằng nhau nên chu vi bằng nhau
(vì p = 
= p').
Suy ra các cạnh còn lại bằng nhau: AB = BC. Vì hai tam giác đó được chọn bất kì nên AB = BC = CD = DA và ABCD là hình thoi.
Trước hết, ta chứng minh bài toán sau đây:
"Cho hai tam giác ABC và AMN với 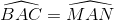, các bán kính đường tròn nội tiếp bằng nhau. Chứng minh rằng nếu AB < AM thì AC > AN"
Dựng các tam giác đó như trong hình vẽ sau, trong đó giả sử AC < AN tiếp điểm của BC với đường tròn nội tiếp tam giác ABC là I.
Ta thấy ngay mọi điểm của (O) đều nằm trên nửa mặt phẳng bờ BC có chứa điểm A. Trong đó M, N lần lượt nằm trên các tia đối của tia BA, CA. Suy ra đoạn thẳng MN nằm trên nửa mặt phẳng bờ BC không chứa A, và do đó không có điểm chung với (O) trái với giả thiết và bài toán đã được chứng minh.
Giả sử IA < IC (1), áp dựng bài toán vừa nêu cho ∆ AIB và ∆ CID, ta có: IB > ID hay ID < IB. Lại áp dụng cho tam giác ∆ IAD và ∆ ICB, ta có IA > IC, mâu thuẫn với (1). Vậy IA > IC.
Chứng minh tương tự, ta cũng có IC > IA. Suy ra IA = IC. Một cách tương tự, ta cũng có IB = ID. Vì có cạnh IB chung và IA = IC nên hai tam giác IAB, ICB có diện tích bằng nhau, lại có bán kính đường tròn nội tiếp bằng nhau nên chu vi bằng nhau
(vì p = = p').
Suy ra các cạnh còn lại bằng nhau: AB = BC. Vì hai tam giác đó được chọn bất kì nên AB = BC = CD = DA và ABCD là hình thoi.
Câu hỏi liên quan
-
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Rút gọn A
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Tính giá trị biểu thức của A với x =
-
Tìm b để A =
-
Cho hệ phương trình:
Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-
Chứng minh rằng: AM2 = AN.AB
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào