Cho tam giác ABC nội tiếp một đường tròn (O) và một điểm M nằm trên (O). Gọi H, I, K theo thứ tự là chân các đường vuông góc hạ từ M xuống các đường thẳng AB, BC, CA. Chứng minh rằng H, I, K thẳng hàng.
Câu hỏi
Nhận biếtCho tam giác ABC nội tiếp một đường tròn (O) và một điểm M nằm trên (O). Gọi H, I, K theo thứ tự là chân các đường vuông góc hạ từ M xuống các đường thẳng AB, BC, CA. Chứng minh rằng H, I, K thẳng hàng.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Giả sử I nằm ngoài đường thẳng BC. H nằm giữa A, B. Suy ra I, H nằm trên hai nửa mặt phẳng bờ AC đối nhau. Do đó, nếu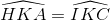 
thì H, K, I thẳng hàng (1).
Ta có các tứ giác HAMK, KMIC nội tiếp được
(vì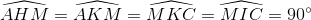 
). Còn tứ giác MABC thì nội tiếp (O). Một mặt ta có 
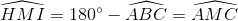(2) hiển nhiên MC cắt HI tại một điểm nằm giữa K, I mà K nằm giữa H, I nên tia MC nằm giữa các tia MA, MI. Kết hợp với (2) ta có:
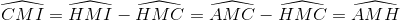
Suy ra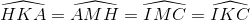 
Kết hợp với (1) ta có H, K, I thẳng hàng.
Giả sử I nằm ngoài đường thẳng BC. H nằm giữa A, B. Suy ra I, H nằm trên hai nửa mặt phẳng bờ AC đối nhau. Do đó, nếu 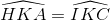thì H, K, I thẳng hàng (1).
Ta có các tứ giác HAMK, KMIC nội tiếp được
(vì 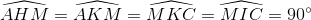). Còn tứ giác MABC thì nội tiếp (O). Một mặt ta có 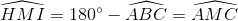(2) hiển nhiên MC cắt HI tại một điểm nằm giữa K, I mà K nằm giữa H, I nên tia MC nằm giữa các tia MA, MI. Kết hợp với (2) ta có:
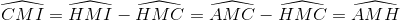
Suy ra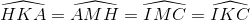
Kết hợp với (1) ta có H, K, I thẳng hàng.
Câu hỏi liên quan
-
Giải phương trình với a = -2
-
Rút gọn biểu thức A
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Giải phương trình (1) khi m = -5
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Chứng minh rằng: AM2 = AN.AB
-
Tính giá trị biểu thức của A với x =
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.