Gọi K là giao điểm thứ hai của đường thẳng DC với đường tròn(O) . Tứ giác MIKD là hình gì? Tại sao?

Câu hỏi
Nhận biếtGọi K là giao điểm thứ hai của đường thẳng DC với đường tròn(O) . Tứ giác MIKD là hình gì? Tại sao?
Đáp án đúng: A
Lời giải của Luyện Tập 365
Tia đối của tia MA là tia phân giác của góc CMD mà ∆ MCD cân
=> MA ┴ CD => MI // KD => 
=> 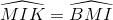 (so le trong) nên IK // MD
(so le trong) nên IK // MD
Vậy MIKD là hình bình hành.
Tia đối của tia MA là tia phân giác của góc CMD mà ∆ MCD cân
=> MA ┴ CD => MI // KD => ![]()
=> 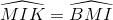 (so le trong) nên IK // MD
(so le trong) nên IK // MD
Vậy MIKD là hình bình hành.
Câu hỏi liên quan
-

Tìm m để phương trình (1) có nghiệm .
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Chứng minh rằng: AM2 = AN.AB
-

Rút gọn A
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Chứng minh DM.CE=DE.CM
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
