Cho tam giác ABC, BC = a, 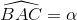 . Hai tam giác ABC phải thỏa mãn điều kiện gì để chu vi của nó đạt giá trị lớn nhất
. Hai tam giác ABC phải thỏa mãn điều kiện gì để chu vi của nó đạt giá trị lớn nhất

Câu hỏi
Nhận biếtCho tam giác ABC, BC = a, 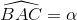 . Hai tam giác ABC phải thỏa mãn điều kiện gì để chu vi của nó đạt giá trị lớn nhất
. Hai tam giác ABC phải thỏa mãn điều kiện gì để chu vi của nó đạt giá trị lớn nhất
Đáp án đúng: A
Lời giải của Luyện Tập 365
Tập hợp đỉnh A là cung chứa góc 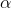 vẽ trên đoạn BC cố định và bằng a (hình vẽ). Gọi
vẽ trên đoạn BC cố định và bằng a (hình vẽ). Gọi 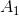 là điểm chính giữa của cung lớn BC
là điểm chính giữa của cung lớn BC 
Xét điểm A bất kì trên cung 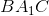 , lấy điểm C' trên tia đối của tia AB và AC'= AC, ta có
, lấy điểm C' trên tia đối của tia AB và AC'= AC, ta có 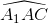 =
=  sđ
sđ 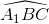 ;
; 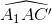 =
=  sđ (cung A1A + cung AC + cung BC)
sđ (cung A1A + cung AC + cung BC)
= 
=> 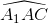 =>
=> 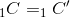 (c.g.c)
(c.g.c)
Ta lại có BA1 + A1C = BA1 + A1C’ > BC’ = AB + AC
Chu vi ∆ A1BC > chu vi ∆ ABC.
Vậy chu vi ∆ A1BC là chu vi lớn nhất cần tìm.

Tập hợp đỉnh A là cung chứa góc 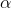 vẽ trên đoạn BC cố định và bằng a (hình vẽ). Gọi
vẽ trên đoạn BC cố định và bằng a (hình vẽ). Gọi ![]() là điểm chính giữa của cung lớn BC
là điểm chính giữa của cung lớn BC ![]()
Xét điểm A bất kì trên cung 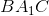 , lấy điểm C' trên tia đối của tia AB và AC'= AC, ta có
, lấy điểm C' trên tia đối của tia AB và AC'= AC, ta có ![]() =
=  sđ
sđ ![]() ;
; ![]() =
=  sđ (cung A1A + cung AC + cung BC)
sđ (cung A1A + cung AC + cung BC)
= ![]()
=> 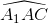 =>
=> 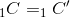 (c.g.c)
(c.g.c)
Ta lại có BA1 + A1C = BA1 + A1C’ > BC’ = AB + AC
Chu vi ∆ A1BC > chu vi ∆ ABC.
Vậy chu vi ∆ A1BC là chu vi lớn nhất cần tìm.

Câu hỏi liên quan
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Rút gọn biểu thức A
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Giải hệ phương trình

-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Chứng minh DM.CE=DE.CM
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
