Cho hai đường tròn (O1;R1) và (O2;R2) (R1<R2) tiếp xúc ngoài với nhau tại A .Kẻ các đường kính AO1Bvà AO2C.Gọi DElà tiếp tuyến chung ngoài của hai đường tròn (D∈(O1),E∈(O2)).Gọi M là giao điểm của BD và CE. Trả lời câu hỏi dưới đây:Gọi (O;R)tiếp xuc với DE đồng thời tiếp xúc ngoài với (O1;R1) và (O2;R2). Chứng minh rằng :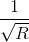 =
=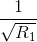 +
+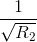

Câu hỏi
Nhận biếtCho hai đường tròn (O1;R1) và (O2;R2) (R1<R2) tiếp xúc ngoài với nhau tại A .Kẻ các đường kính AO1Bvà AO2C.Gọi DElà tiếp tuyến chung ngoài của hai đường tròn (D∈(O1),E∈(O2)).Gọi M là giao điểm của BD và CE.
Trả lời câu hỏi dưới đây:
Gọi (O;R)tiếp xuc với DE đồng thời tiếp xúc ngoài với (O1;R1) và (O2;R2). Chứng minh rằng :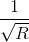 =
=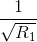 +
+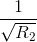
Đáp án đúng: B
Lời giải của Luyện Tập 365
* Xét bài toán phụ :Cho (O;R) và (O';R')tiếp xúc ngoài với nhau tại A (R>R').Nếu BC là tiếp tuyến chung ngoài của hai đờng tròn (B ∈(O),C ∈(O')) thì BC = 2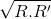

Thật vậy ,kẻ O’Q⊥ OB (Q∈OB) thì tứ giác BCO’Q là hình chữ nhật => BC= O’Q và OQ = R-R’.Theo định lí pitago trong tam giác vuông OO’Q ta có :
BC = O’O = 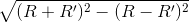 = 2
= 2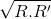 (đpcm)
(đpcm)
*Trở lại bài toán :Gọi (O) tiếp xúc với DE tại T.Theo bài toán phụ ta có:

DT = 2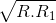
TE=2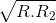
DE= 2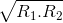
Mà DT+TE=DE
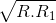 +
+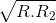 =
=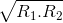
<=>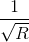 =
=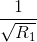 +
+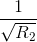 ( đpcm)
( đpcm)
* Xét bài toán phụ :Cho (O;R) và (O';R')tiếp xúc ngoài với nhau tại A (R>R').Nếu BC là tiếp tuyến chung ngoài của hai đờng tròn (B ∈(O),C ∈(O')) thì BC = 2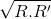

Thật vậy ,kẻ O’Q⊥ OB (Q∈OB) thì tứ giác BCO’Q là hình chữ nhật => BC= O’Q và OQ = R-R’.Theo định lí pitago trong tam giác vuông OO’Q ta có :
BC = O’O = 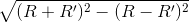 = 2
= 2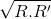 (đpcm)
(đpcm)
*Trở lại bài toán :Gọi (O) tiếp xúc với DE tại T.Theo bài toán phụ ta có:

DT = 2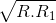
TE=2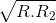
DE= 2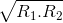
Mà DT+TE=DE
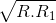 +
+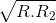 =
=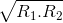
<=>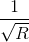 =
=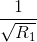 +
+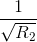 ( đpcm)
( đpcm)
Câu hỏi liên quan
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Giải phương trình (1) khi m = -5
-

Tính giá trị biểu thức của A với x =

-

Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Chứng minh DM.CE=DE.CM
-

Tìm b để A =

-

Giải hệ phương trình với a = 2
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Rút gọn biểu thức A
