Hãy xét vị trí tương đối của hai đường thẳng AO và PQ.
Câu hỏi
Nhận biếtHãy xét vị trí tương đối của hai đường thẳng AO và PQ.
Đáp án đúng: C
Lời giải của Luyện Tập 365
TA có PC ⊥ MQ; QB ⊥ MP (chứng minh trên) nên giao điểm N của PC với QB là trực tâm của tam giác MPQ. Suy ra MN ⊥ PQ.
Mà ta lại có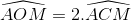 
= 2 . 45o = 90o(góc ở tâm và góc nội tiếp cùng chắn cung AM), hay AO ⊥ MN.
Vậy AO // PQ (vì cùng vuông góc với MN);
(trường hợp ∆ ABC cân đỉnh A thì OA = PQ).
TA có PC ⊥ MQ; QB ⊥ MP (chứng minh trên) nên giao điểm N của PC với QB là trực tâm của tam giác MPQ. Suy ra MN ⊥ PQ.
Mà ta lại có 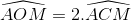= 2 . 45o = 90o(góc ở tâm và góc nội tiếp cùng chắn cung AM), hay AO ⊥ MN.
Vậy AO // PQ (vì cùng vuông góc với MN);
(trường hợp ∆ ABC cân đỉnh A thì OA = PQ).
Câu hỏi liên quan
-
Chứng minh DM.CE=DE.CM
-
Rút gọn A
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Tính giá trị biểu thức của A với x =
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Chứng minh rằng: AM2 = AN.AB
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Giải hệ phương trình
-
Tìm a để phương trình có 2 nghiệm nguyên