Cho tam giác cân ABC (AB = AC) các đường tròn đường kính AC, AB cắt AB tại H, cắt AC tại K. Một đường thẳng xy qua A cắt đường tròn thứ nhất ở D, đường tròn thứ hai ở E. Trả lời câu hỏi dưới đây:Chứng minh tam giác NDE cân.

Câu hỏi
Nhận biếtCho tam giác cân ABC (AB = AC) các đường tròn đường kính AC, AB cắt AB tại H, cắt AC tại K. Một đường thẳng xy qua A cắt đường tròn thứ nhất ở D, đường tròn thứ hai ở E.
Trả lời câu hỏi dưới đây:
Chứng minh tam giác NDE cân.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có : cung KD = cung CE (1) (vì các cung trương 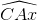 trên hai đường tròn bằng nhau, tương tự ta có cung NK = cung NC
trên hai đường tròn bằng nhau, tương tự ta có cung NK = cung NC
=> 
=> Cung ND = Cung NE trên hai đường tròn bằng nhau, suy ra ND = NE
=> ∆ NDE cân.
Ta có : cung KD = cung CE (1) (vì các cung trương ![]() trên hai đường tròn bằng nhau, tương tự ta có cung NK = cung NC
trên hai đường tròn bằng nhau, tương tự ta có cung NK = cung NC
=> ![]()
=> Cung ND = Cung NE trên hai đường tròn bằng nhau, suy ra ND = NE
=> ∆ NDE cân.
Câu hỏi liên quan
-

Giải phương trình (1) khi m = -5
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Giải phương trình với a = -2
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Giải hệ phương trình với a = 2
-

Rút gọn biểu thức A
