Tìm phần nguyên của tổng A + B (kí hiệu là [A + B]). (Phần nguyên của các số thực a, được kí hiệu là [a] là số nguyên lớn nhất không vượt quá a. Chẳng hạn: [3] = 3, [2,5] = 2; [-3,7] = -4; [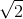 ] = 1, [
] = 1, [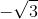 ] = -2 Phần lẻ của các số thực a được kí hiệu là {a} và {a} = a - [a] ).
] = -2 Phần lẻ của các số thực a được kí hiệu là {a} và {a} = a - [a] ).
![Tìm phần nguyên của tổng A + B (kí hiệu là [A + B]). (Phần nguyên của các số thực a, được Tìm phần nguyên của tổng A + B (kí hiệu là [A + B]). (Phần nguyên của các số thực a, được](https://luyentap365.com/wp-content/themes/luyentap365/assets/images/tong-hop-cac-cau-hoi-on-tap-luyen-thi.png)
Câu hỏi
Nhận biếtTìm phần nguyên của tổng A + B (kí hiệu là [A + B]). (Phần nguyên của các số thực a, được kí hiệu là [a] là số nguyên lớn nhất không vượt quá a. Chẳng hạn: [3] = 3, [2,5] = 2; [-3,7] = -4; [![]() ] = 1, [
] = 1, [![]() ] = -2 Phần lẻ của các số thực a được kí hiệu là {a} và {a} = a - [a] ).
] = -2 Phần lẻ của các số thực a được kí hiệu là {a} và {a} = a - [a] ).
Đáp án đúng: D
Lời giải của Luyện Tập 365
Theo trên ta có:
A + B < 5 và A + B > ![\sqrt{6}+\sqrt[3]{6}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47161_561956_1.gif) > 2,4 + 1,8 = 4,2
> 2,4 + 1,8 = 4,2
Vậy [A + B] = 4.
Theo trên ta có:
A + B < 5 và A + B > ![\sqrt{6}+\sqrt[3]{6}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47161_561956_1.gif) > 2,4 + 1,8 = 4,2
> 2,4 + 1,8 = 4,2
Vậy [A + B] = 4.
Câu hỏi liên quan
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Tính giá trị biểu thức của A với x =

-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Chứng minh rằng: AM2 = AN.AB
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Giải hệ phương trình với a = 2
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
