Cho các số: A = 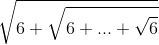 B =
B = ![\sqrt[3]{6+\sqrt[3]{6+...+\sqrt[3]{6}}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0619/51595_233193_2.gif) Trong mỗi số đều có 2001 dấu căn. Trả lời câu hỏi dưới đây:Chứng minh rằng các số A, B đều không phải là các số nguyên.
Trong mỗi số đều có 2001 dấu căn. Trả lời câu hỏi dưới đây:Chứng minh rằng các số A, B đều không phải là các số nguyên.

Câu hỏi
Nhận biếtCho các số: A = 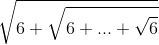
B = ![\sqrt[3]{6+\sqrt[3]{6+...+\sqrt[3]{6}}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0619/51595_233193_2.gif)
Trong mỗi số đều có 2001 dấu căn.
Trả lời câu hỏi dưới đây:
Chứng minh rằng các số A, B đều không phải là các số nguyên.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có: 2 < √6 < A < 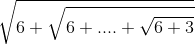 = 3
= 3
và 1 < ![\sqrt[3]{6}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47160_548320_3.gif) < B <
< B < ![\sqrt[3]{6+\sqrt[3]{6}+...+\sqrt[3]{6+2}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47160_461310_4.gif) = 2
= 2
Từ đó suy ra điều cần chứng minh.
Ta có: 2 < √6 < A < 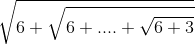 = 3
= 3
và 1 < ![\sqrt[3]{6}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47160_548320_3.gif) < B <
< B < ![\sqrt[3]{6+\sqrt[3]{6}+...+\sqrt[3]{6+2}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0420/v47160_461310_4.gif) = 2
= 2
Từ đó suy ra điều cần chứng minh.
Câu hỏi liên quan
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Giải phương trình với a = -2
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Rút gọn A
-

Rút gọn biểu thức A
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Tìm m để phương trình (1) có nghiệm .
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
