Các đường cao của tam giác ABC có phương trình là x + y = 2, 9x - 3y = 4 tọa độ đỉnh A(2; 2). Lập phương trình các cạnh ∆ABC.

Câu hỏi
Nhận biếtCác đường cao của tam giác ABC có phương trình là x + y = 2, 9x - 3y = 4 tọa độ đỉnh A(2; 2). Lập phương trình các cạnh ∆ABC.
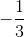 x +
x +  ; AC: y = x + 1; BC: y = -
; AC: y = x + 1; BC: y = -  x +
x + 
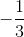 x +
x +  ; AC: y = x; BC: y = -
; AC: y = x; BC: y = -  x +
x + 
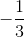 x +
x +  ; AC: y = 2x; BC: y = -
; AC: y = 2x; BC: y = -  x +
x + 
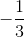 x +
x +  ; AC: y = x - 1; BC: y = -
; AC: y = x - 1; BC: y = -  x +
x + 
Đáp án đúng: B
Lời giải của Luyện Tập 365
Thay tọa độ A(2;2) vào các phương trình đã cho không thấy thỏa mãn, nên một đường là đường cao BI(x + y = 2) và một đường cao CK (9x - 3y = 4)
Vì AB ⊥ CK nên phương trình của AB là y = 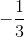 x +
x +  . Tương tự phương trình của cạnh AC là y = x.
. Tương tự phương trình của cạnh AC là y = x.
H là trực tâm của ∆ABC nên là giao điêm hai đường cao BI và CK. Tọa độ H là nghiệm của hệ phương trình:
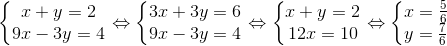
H là 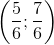 phương trình đường cao AH là y =
phương trình đường cao AH là y =  x +
x + 
Từ đó suy ra phương trình của BC là y= - x +
x + 
Thay tọa độ A(2;2) vào các phương trình đã cho không thấy thỏa mãn, nên một đường là đường cao BI(x + y = 2) và một đường cao CK (9x - 3y = 4)
Vì AB ⊥ CK nên phương trình của AB là y = 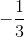 x +
x +  . Tương tự phương trình của cạnh AC là y = x.
. Tương tự phương trình của cạnh AC là y = x.
H là trực tâm của ∆ABC nên là giao điêm hai đường cao BI và CK. Tọa độ H là nghiệm của hệ phương trình:
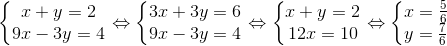
H là 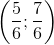 phương trình đường cao AH là y =
phương trình đường cao AH là y =  x +
x + 
Từ đó suy ra phương trình của BC là y= - x +
x + 
Câu hỏi liên quan
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

Tìm m để phương trình (1) có nghiệm .
-

Rút gọn A
-

Giải phương trình (1) khi m = -5
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Giải hệ phương trình

-

Tìm b để A =

-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
