Cho hai đường thẳng y = a1x + b1 (d1) và y = a2x + b2 (d2) vẽ trên cùng một mặt phẳng tọa độ. Chứng minh rằng (d1) và (d2) vuông góc với nhau khi và chỉ khi a1.a2 = -1

Câu hỏi
Nhận biếtCho hai đường thẳng y = a1x + b1 (d1) và y = a2x + b2 (d2) vẽ trên cùng một mặt phẳng tọa độ. Chứng minh rằng (d1) và (d2) vuông góc với nhau khi và chỉ khi a1.a2 = -1
Đáp án đúng: A
Lời giải của Luyện Tập 365
Cho hai đường thẳng:
y = a1x + b1 (d1)
y = a2x + b2 (d2)
Ta phải chứng minh (d1) ⊥ (d2) => a1.a2 = -1
Qua O vẽ hai đường thẳng :
(d'1) : y = a1x
(d'2) : y = a2x
Hiển nhiên (d1) // (d'1) , (d2) // (d'2).
+) Trước tiên ta chứng minh (d1) ⊥ (d2) => a1.a2 = -1.
Giả sử a1 > 0 (không làm mất tính tổng quát của bài toán) suy ra a2 < 0
(vì (d'1) ⊥ (d'2)).
Đường thẳng (d'1) đi qua điểm A(1; a1 )
Đường thẳng (d'2) đi qua điểm B (1; a2)
Hiển nhiên AB // Oy nên AB ⊥ Ox tại I có OI = 1. Vì (d'1) ⊥ (d'2)
=> góc AOB là góc vuông. Trong tam giác vuông AOB , OI là đường cao thuộc cạnh huyền , vậy ta có:
IA.IB = OI2 = 1 => a1.|a2| = 1
Vì a2 < 0 nên - a1.a2 = 1 hay a1.a2 = -1
+) Ngược lại, với a1.a2 = -1 ta phải chứng minh (d'1) ⊥ (d'2)
Thật vậy, nếu a1.a2 = -1 => a1.|a2| = 1.
=> IA.IB = OI2
=> 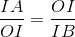 => ∆ IAO
=> ∆ IAO 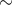 ∆IOB
∆IOB
=> 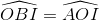 mà
mà 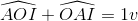 =>
=> 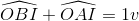
=> Góc AOB là góc vuông hay (d'1) ⊥ (d'2)
Ghi chú: Sau này khi lên học lớp trên ta sẽ chứng minh được công thức sau. Gọi  là góc tạo bởi hai đường thẳng
là góc tạo bởi hai đường thẳng 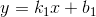 và
và 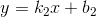 thì
thì
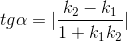 khi
khi 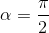 thì
thì 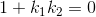 <=>
<=> 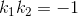

Cho hai đường thẳng:
y = a1x + b1 (d1)
y = a2x + b2 (d2)
Ta phải chứng minh (d1) ⊥ (d2) => a1.a2 = -1
Qua O vẽ hai đường thẳng :
(d'1) : y = a1x
(d'2) : y = a2x
Hiển nhiên (d1) // (d'1) , (d2) // (d'2).
+) Trước tiên ta chứng minh (d1) ⊥ (d2) => a1.a2 = -1.
Giả sử a1 > 0 (không làm mất tính tổng quát của bài toán) suy ra a2 < 0
(vì (d'1) ⊥ (d'2)).
Đường thẳng (d'1) đi qua điểm A(1; a1 )
Đường thẳng (d'2) đi qua điểm B (1; a2)
Hiển nhiên AB // Oy nên AB ⊥ Ox tại I có OI = 1. Vì (d'1) ⊥ (d'2)
=> góc AOB là góc vuông. Trong tam giác vuông AOB , OI là đường cao thuộc cạnh huyền , vậy ta có:
IA.IB = OI2 = 1 => a1.|a2| = 1
Vì a2 < 0 nên - a1.a2 = 1 hay a1.a2 = -1
+) Ngược lại, với a1.a2 = -1 ta phải chứng minh (d'1) ⊥ (d'2)
Thật vậy, nếu a1.a2 = -1 => a1.|a2| = 1.
=> IA.IB = OI2
=> 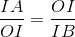 => ∆ IAO
=> ∆ IAO 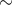 ∆IOB
∆IOB
=> 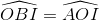 mà
mà 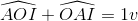 =>
=> 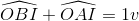
=> Góc AOB là góc vuông hay (d'1) ⊥ (d'2)
Ghi chú: Sau này khi lên học lớp trên ta sẽ chứng minh được công thức sau. Gọi 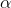 là góc tạo bởi hai đường thẳng
là góc tạo bởi hai đường thẳng 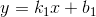 và
và 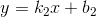 thì
thì
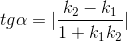 khi
khi 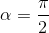 thì
thì 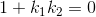 <=>
<=> 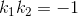

Câu hỏi liên quan
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Chứng minh DM.CE=DE.CM
-

Chứng minh rằng: AM2 = AN.AB
