Đơn giản biểu thức: A = ![\frac{\sqrt[3]{a^{4}}+\sqrt[3]{a^{2}b^{2}}+\sqrt[3]{b^{4}}}{\sqrt[3]{a^{2}}+\sqrt[3]{ab}+\sqrt[3]{b^{2}}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_286904_1.gif)

Câu hỏi
Nhận biếtĐơn giản biểu thức: A = ![\frac{\sqrt[3]{a^{4}}+\sqrt[3]{a^{2}b^{2}}+\sqrt[3]{b^{4}}}{\sqrt[3]{a^{2}}+\sqrt[3]{ab}+\sqrt[3]{b^{2}}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_286904_1.gif)
A.
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_572641_1.gif)
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_572641_1.gif)
B.
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-2\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_248341_1.gif)
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-2\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_248341_1.gif)
C.
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}+2\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_525536_1.gif)
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}+2\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_525536_1.gif)
D.
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}+\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_139672_1.gif)
![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}+\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/42865_139672_1.gif)
Đáp án đúng: A
Lời giải của Luyện Tập 365
Đặt ![\sqrt[3]{a}=x](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_396485_1.gif) ,
, ![\sqrt[3]{b}=y](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_751200_2.gif) ta có A =
ta có A = 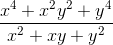
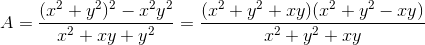
= x2 + y2 - xy
Nên ![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_453581_6.gif)
Đặt ![\sqrt[3]{a}=x](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_396485_1.gif) ,
, ![\sqrt[3]{b}=y](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_751200_2.gif) ta có A =
ta có A = 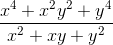
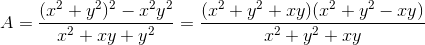
= x2 + y2 - xy
Nên ![A=\sqrt[3]{a^{2}}+\sqrt[3]{b^{2}}-\sqrt[3]{ab}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0407/v39372_453581_6.gif)
Câu hỏi liên quan
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Giải phương trình với a = -2
-

Rút gọn A
-

Tìm m để phương trình (1) có nghiệm .
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Tìm a để phương trình có 2 nghiệm nguyên
