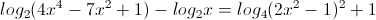Tìm số phức có modun nhỏ nhất sao cho: |z| = |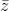 - 3 + 4i|
- 3 + 4i|

Câu hỏi
Nhận biếtTìm số phức có modun nhỏ nhất sao cho: |z| = |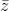 - 3 + 4i|
- 3 + 4i|
 - 2i
- 2i  + 2i
+ 2i  - 2i
- 2i  + 2i
+ 2i Đáp án đúng: D
Lời giải của Luyện Tập 365
Gọi số phức z có dạng z = x + yi, với x, y ∈ R
Khi đó |z| = |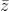 - 3 + 4i|
- 3 + 4i|
⇔ |x + yi| = |x – yi – 3 + 4i| ⇔ |x + yi| = |x – 3 + (4 – y)i|
⇔ x2 + y2 = (x – 3)2 + (4 – y)2 ⇔ 6x + 8y = 25. <=> y = 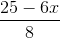
|z| = 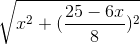 =
= 
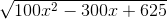 ≥
≥ 
Số phức z có modun nhỏ nhất đạt được khi x =  và y = 2
và y = 2
Vậy z =  + 2i
+ 2i
Gọi số phức z có dạng z = x + yi, với x, y ∈ R
Khi đó |z| = |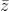 - 3 + 4i|
- 3 + 4i|
⇔ |x + yi| = |x – yi – 3 + 4i| ⇔ |x + yi| = |x – 3 + (4 – y)i|
⇔ x2 + y2 = (x – 3)2 + (4 – y)2 ⇔ 6x + 8y = 25. <=> y = 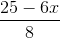
|z| = 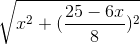 =
= 
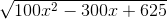 ≥
≥ 
Số phức z có modun nhỏ nhất đạt được khi x =  và y = 2
và y = 2
Vậy z =  + 2i
+ 2i
Câu hỏi liên quan
-

Giải phương trình
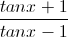 =
=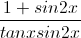
-

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x - y + z - 2 = 0, (β): x + 2y +2z - 4 = 0. Viết phương trình đường thẳng d nằm trong (α), song song với (β) và cách (β) một khoảng bằng 1.
-

Trong mặt phẳng với hệ trục Oxy, cho điểm M(4; -3) và đường tròn (C): x2 + y2 - 4x - 2y +1 = 0 với tâm là I. Lập phương trình tổng quát của đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm phân biệt P, Q sao cho tam giác IPQ vuông.
-

Cho các số thực x, y, z không âm thỏa mãn điều kiện x3 + y3 + z3= 2 + 3xyz. Tìm giá trị nhỏ nhất của biểu thức P = x2 + 2y2 + 3z2.
-

Một hộp đựng 5 viên bi đỏ, 6 viên xanh và 7 viên bi vàng. Chọn ra 5 viên bi rừ hộp đó. Hỏi có bao nhiêu cách chọn mà 5 viên bi được chọn không có đủ cả 3 màu?
-

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Cho các số thực x, y thỏa mãn điều kiện x+y=
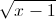 +
+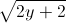 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=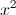 +
+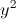 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8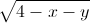
-

Tìm số phức z thỏa mãn
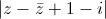 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 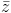 ) là số ảo.
) là số ảo. -

Giải phương trình (1-
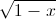 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Giải phương trình: