Chứng minh rằng: 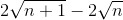 <
< 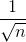 <
< 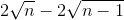 . Từ đó suy ra: 2004 < 1 +
. Từ đó suy ra: 2004 < 1 + 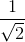 +
+ 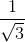 + ..... +
+ ..... + 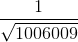 < 2005
< 2005

Câu hỏi
Nhận biếtChứng minh rằng: 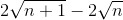 <
< 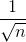 <
< 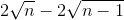 . Từ đó suy ra: 2004 < 1 +
. Từ đó suy ra: 2004 < 1 + 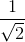 +
+ 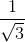 + ..... +
+ ..... + 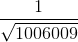 < 2005
< 2005
Đáp án đúng: A
Lời giải của Luyện Tập 365
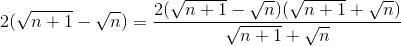
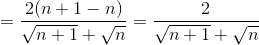 <
< 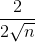
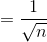
(vì 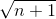 >
> 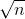 )
)
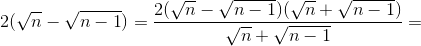
![=\frac{2[n-(n-1)]}{\sqrt{n}+\sqrt{n-1}}=\frac{2}{\sqrt{n}+\sqrt{n-1}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0404/v38529_931951_8.gif) >
> 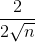
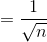
Do đó 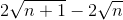 <
< 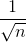 <
< 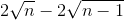
Áp dụng hệ thức (*) ta có:
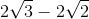 <
< 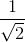 <
< 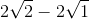
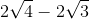 <
< 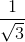 <
< 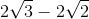
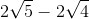 <
< 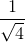 <
< 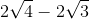
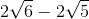 <
< 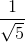 <
< 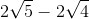
..............................................................
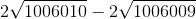 <
< 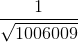 <
< 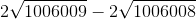
Cộng hai vế của các bất đẳng thức trên ta có:
2006 - 3 < 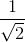 +
+ 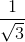 +
+ 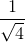 + ....... +
+ ....... + 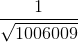 < 2006 -2
< 2006 -2
Vậy 2004 < 1 + 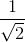 +
+ 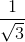 + ..... +
+ ..... + 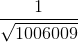 < 2005
< 2005
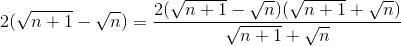
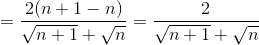 <
< 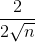
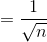
(vì 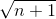 >
> 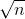 )
)
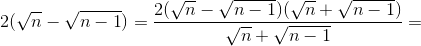
![=\frac{2[n-(n-1)]}{\sqrt{n}+\sqrt{n-1}}=\frac{2}{\sqrt{n}+\sqrt{n-1}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0404/v38529_931951_8.gif) >
> 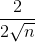
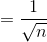
Do đó 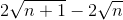 <
< 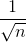 <
< 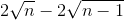
Áp dụng hệ thức (*) ta có:
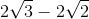 <
< 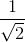 <
< 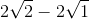
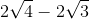 <
< 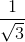 <
< 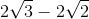
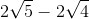 <
< 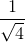 <
< 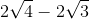
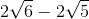 <
< 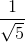 <
< 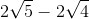
..............................................................
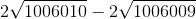 <
< 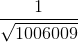 <
< 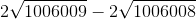
Cộng hai vế của các bất đẳng thức trên ta có:
2006 - 3 < 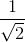 +
+ 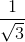 +
+ 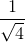 + ....... +
+ ....... + 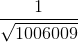 < 2006 -2
< 2006 -2
Vậy 2004 < 1 + 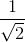 +
+ 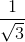 + ..... +
+ ..... + 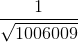 < 2005
< 2005
Câu hỏi liên quan
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Giải phương trình với a = -2
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Tìm b để A =

-

Chứng minh rằng: AM2 = AN.AB
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Rút gọn A
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
