So sánh các số: Trả lời câu hỏi dưới đây: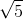 và
và 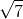

Câu hỏi
Nhận biếtSo sánh các số:
Trả lời câu hỏi dưới đây:
![]() và
và ![]()
A.
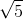 >
> 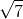
B.
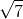 -
- 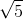 =
= 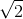
C.
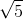 <
< 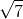
D.
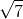 -
- 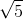 = 2
= 2
Đáp án đúng: C
Lời giải của Luyện Tập 365
Ta có 5 < 7 <=> 5 - 7 < 0
<=> 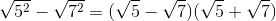 < 0
< 0
<=> 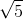 -
- 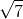 < 0 (do
< 0 (do 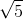 +
+ 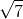 > 0)
> 0)
<=> 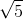 <
< 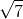
Ta có 5 < 7 <=> 5 - 7 < 0
<=> 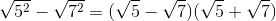 < 0
< 0
<=> ![]() -
- ![]() < 0 (do
< 0 (do ![]() +
+ ![]() > 0)
> 0)
<=> ![]() <
< ![]()
Câu hỏi liên quan
-

Giải hệ phương trình với a = 2
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Tìm b để A =

-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

Tìm m để phương trình (1) có nghiệm .
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Rút gọn biểu thức A
