Người II đi trên đường từ B đến M rồi đi trên cánh đồng từ M đến D và gặp người I tại D như hình 3, sao cho thòi gian chuyển động của hai người đến ỉúc gặp nhau là ngắn nhất. Tìm thòi gian chuyển động này và các khoảng cách BM, AD 
Câu hỏi
Nhận biếtNgười II đi trên đường từ B đến M rồi đi trên cánh đồng từ M đến D và gặp người I tại D như hình 3, sao cho thòi gian chuyển động của hai người đến ỉúc gặp nhau là ngắn nhất. Tìm thòi gian chuyển động này và các khoảng cách BM, AD
Đáp án đúng: A
Lời giải của Luyện Tập 365
Gọi t' là thời gian chuyển động của hai người khi đến D; X là thời gian người E chuyến động trên đường BM.
Ta có AD = v1t'; BM = v2’x; MD = v2(t' - x) và:
MD2=(AD-BM)2 + AB2 hay [v2(t’ - x)]2 = (v1t’ - v2'x)2 + l2[5(t' - x)]2 = (4t’-13x)2 + 5402 (25t'2 - 100t'x + 25x2)
= 16t’2-104t'x + 169x2+291600
<=> 144x2 - 54t'x + 291600 - 9t2 = 0
Đế phương trình trên có nghiệm thì: ∆' ≤ 0 hay (27)t’2 - 144(291600 - 9t’2) ≤ 0 Suy ra t' > 144s hay tmin=144s và x=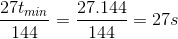
BM = v2’x = 13.27 = 351m; AD – v1tmin= 4.144 = 576m.
Vậy: Thời gian ngắn nhất đế hai người gặp nhau ở D là tmin= 144s; các khoảng cách BM và AD là BM = 351m, AD = 576m.
Gọi t' là thời gian chuyển động của hai người khi đến D; X là thời gian người E chuyến động trên đường BM.
Ta có AD = v1t'; BM = v2’x; MD = v2(t' - x) và:
MD2=(AD-BM)2 + AB2 hay [v2(t’ - x)]2 = (v1t’ - v2'x)2 + l2[5(t' - x)]2 = (4t’-13x)2 + 5402 (25t'2 - 100t'x + 25x2)
= 16t’2-104t'x + 169x2+291600
<=> 144x2 - 54t'x + 291600 - 9t2 = 0
Đế phương trình trên có nghiệm thì: ∆' ≤ 0 hay (27)t’2 - 144(291600 - 9t’2) ≤ 0 Suy ra t' > 144s hay tmin=144s và x=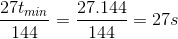
BM = v2’x = 13.27 = 351m; AD – v1tmin= 4.144 = 576m.
Vậy: Thời gian ngắn nhất đế hai người gặp nhau ở D là tmin= 144s; các khoảng cách BM và AD là BM = 351m, AD = 576m.
Câu hỏi liên quan
-
Vẽ ảnh của vật AB qua thấu kính L.
-
Điều chỉnh con chạy C để đèn sáng bình thường, hỏi con chạy C đã chia biến trở thành hai phần có tỉ lệ như thế nào?
-
Sau thấu kính L1 người ta đặt một thấu kính phân kì L2 có tiêu cự f2 = . Thấu kính L2 cách thấu kính L1 một khoảng O1O2 = , trục chính của thấu kính trùng nhau (Hình vẽ 3). Vẽ ảnh của vật AB qua hai thấu kính trên và dùng hình học ( không dùng công thức thấu kính) tìm khoảng cách từ ảnh cuối cùng A2B2 đến thấu kính phân kỳ.
-
Thay ròng rọc cố định R bằng một Pa-lăng gồm một ròng rọc cố định R và một ròng rọc cố định R’, đồng thời di chuyển vị trí đứng của người đó về điểm I sao cho
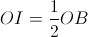(Hình 2) . Người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc) -
Đèn Đ1 và đèn Đ2 ở vị trí nào trong mạch ?
-
Pa-lăng ở câu trên được mắc theo cách khác nhưng vẫn có
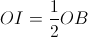(Hình 3) người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc) -
Thay ampe kế bằng vôn kế có điện trở vô cùng lớn. Tìm R3 để số chỉ vôn kế là 16V. Nếu di chuyển con chạy để R3 tăng lên thì số chỉ của vôn kế thay đổi như thế nào?
-
Cố định thấu kính và chùm tia tới, quay gương quanh điểm I một góc α. Điểm sáng S di chuyển thế nào? Tính độ dài quãng đường di chuyển của S theo α.
-
Để cục nước đá chuyển hoàn toàn sang thể hơi ở 1000C thì cần một nhiệt lượng là bao nhiêu kJ? Cho nhiệt dung riêng của nước và nước đá là C1 = 4200J/kg.K; C2 = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.105 J/kg; nhiệt hóa hơi của nước là L = 2,3.106 j/kg.(Bỏ qua sự mất nhiệt với môi trường ngoài).
-
Xét trường hợp khi K đóng : Thay khóa K bằng điện trở R5. Tính R5 để cường độ dòng điện chạy qua điện trở R2 bằng không.