Chứng minh HF là tiếp tuyến của đường tròn (I) đường kính EB

Câu hỏi
Nhận biếtChứng minh HF là tiếp tuyến của đường tròn (I) đường kính EB
A.
Click để xem lời giải chi tiết
Đáp án đúng: A
Lời giải của Luyện Tập 365
∆ HCF cân tại H => 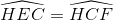
∆ IBF cân tại I => 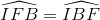
Mà 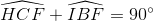 ( ∆ HBC vuông tại H)
( ∆ HBC vuông tại H)
∆ HCF cân tại H => 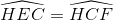
∆ IBF cân tại I => 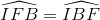
Mà 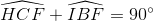 ( ∆ HBC vuông tại H)
( ∆ HBC vuông tại H)
Câu hỏi liên quan
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

Rút gọn A
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-

Giải phương trình với a = -2
-

Giải hệ phương trình với a = 2
-

Rút gọn biểu thức A
-

Chứng minh rằng: AM2 = AN.AB
