Gọi H là trực tâm và O là tâm đường tròn ngoại tiếp tam giac ABC. Tính góc 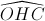

Câu hỏi
Nhận biếtGọi H là trực tâm và O là tâm đường tròn ngoại tiếp tam giac ABC. Tính góc 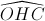
A.
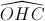 = 400
= 400
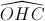 = 400
= 400
B.
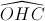 = 900
= 900
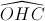 = 900
= 900
C.
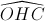 = 300
= 300
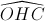 = 300
= 300
D.
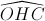 = 600
= 600
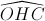 = 600
= 600 Đáp án đúng: C
Lời giải của Luyện Tập 365
Gọi D là giao điểm của CH và AB ta có CD ⊥ AB
Nên 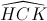 = 900 -
= 900 - 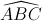 = 300
= 300
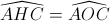 = 1200
= 1200
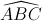 =>
=> 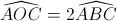 = 1200
= 1200
Ta có 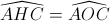 = 1200
= 1200
=> Tứ giác AHOC nội tiếp => 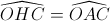
∆OAC cân tại O (vì OA = OC = R) , 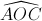 = 1200
= 1200
=> 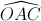 = (1800 – 1200): 2 = 300
= (1800 – 1200): 2 = 300
Vậy 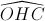 = 300
= 300
Gọi D là giao điểm của CH và AB ta có CD ⊥ AB
Nên 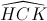 = 900 -
= 900 - 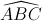 = 300
= 300
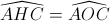 = 1200
= 1200
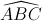 =>
=> 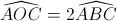 = 1200
= 1200
Ta có 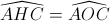 = 1200
= 1200
=> Tứ giác AHOC nội tiếp => 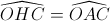
∆OAC cân tại O (vì OA = OC = R) , 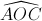 = 1200
= 1200
=> 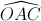 = (1800 – 1200): 2 = 300
= (1800 – 1200): 2 = 300
Vậy 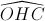 = 300
= 300
Câu hỏi liên quan
-

Giải phương trình với a = -2
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Tìm m để phương trình (1) có nghiệm .
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Chứng minh DM.CE=DE.CM
-

Tìm b để A =

-

Tìm a để phương trình có 2 nghiệm nguyên
-

Chứng minh rằng: AM2 = AN.AB
-

Giải hệ phương trình

