Cho AD = 2R. Tính diện tích tứ giác ABDC theo R.
Câu hỏi
Nhận biếtCho AD = 2R. Tính diện tích tứ giác ABDC theo R.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có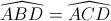 
= 900 (góc nội tiếp chắn nửa đường tròn)
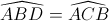(hai góc nội tiếp chắn cung AB)
Mà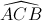 
= 600 (∆ABC đều)
Nên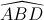 
= 600
∆ABD vuông tại B => AB = AD.sinADB , BD = ADcosADB
AB = 2Rsin600 = √3R, BD = 2Rcos600 = R
Do vậy SABD = 
AB.BD = √3R.R =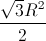 
Tương tự có SACD =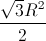
Vậy SABDC = SABD + SACD = √3R2 (đvdt)
Ta có 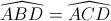= 900 (góc nội tiếp chắn nửa đường tròn)
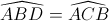(hai góc nội tiếp chắn cung AB)
Mà 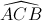= 600 (∆ABC đều)
Nên 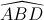= 600
∆ABD vuông tại B => AB = AD.sinADB , BD = ADcosADB
AB = 2Rsin600 = √3R, BD = 2Rcos600 = R
Do vậy SABD = AB.BD = √3R.R =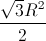
Tương tự có SACD =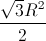
Vậy SABDC = SABD + SACD = √3R2 (đvdt)
Câu hỏi liên quan
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Chứng minh rằng: AM2 = AN.AB
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Rút gọn A
-
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB