Tìm độ cao của cột nước cần đổ vào chậu (tính từ đáy đến mặt thoáng) biết khối lượng riêng của thanh AB và của nước lần lượt là : Dt = 1120 kg/m3 và Dn = 1000 kg/m3?
Câu hỏi
Nhận biếtTìm độ cao của cột nước cần đổ vào chậu (tính từ đáy đến mặt thoáng) biết khối lượng riêng của thanh AB và của nước lần lượt là : Dt = 1120 kg/m3 và Dn = 1000 kg/m3?
Đáp án đúng: C
Lời giải của Luyện Tập 365
Gọi mực nước đổ vào trong chậu để thanh bắt đầu nổi (tính từ B theo chiều dài thanh) là x (cm). ĐK : x < OB = 30cm, theo hình vẽ dưới đây thì x = BI.
Gọi S là tiết diện của thanh, thanh chịu tác dụng của trọng lượng P đặt tại trung điểm M của AB và lực đẩy Acsimet F đặt tại trung điểm N của BI.
Theo điều kiện cân bằng của đòn bẩy thì :
P.MH = F.NK (1) trong đó P = 10m = 10.Dt.S.l
Và F = 10.Dn.S.x
Thay vào (1)
=.> x = . l .
Xét cặp tam giác đồng dạng OMH và ONK ta có = ;
ta tính được MO = MA – OA = 10cm và NO = OB – NB = ;
Thay số và biến đổi để có phương trình bậc 2 theo x :
x2 – 60x + 896 = 0.
Giải phương trình trên và loại nghiệm x = 32 (> 30) ta được x = 28cm.
Từ I hạ IE ⊥ Bx, trong tam giác IBE vuông tại E thì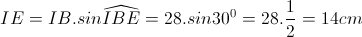 
(cũng có thế sử dụng kiến thức về nửa tam giác đều)
Gọi mực nước đổ vào trong chậu để thanh bắt đầu nổi (tính từ B theo chiều dài thanh) là x (cm). ĐK : x < OB = 30cm, theo hình vẽ dưới đây thì x = BI.
Gọi S là tiết diện của thanh, thanh chịu tác dụng của trọng lượng P đặt tại trung điểm M của AB và lực đẩy Acsimet F đặt tại trung điểm N của BI.
Theo điều kiện cân bằng của đòn bẩy thì :
P.MH = F.NK (1) trong đó P = 10m = 10.Dt.S.l
Và F = 10.Dn.S.x
Thay vào (1)
=.> x = . l .
Xét cặp tam giác đồng dạng OMH và ONK ta có = ;
ta tính được MO = MA – OA = 10cm và NO = OB – NB = ;
Thay số và biến đổi để có phương trình bậc 2 theo x :
x2 – 60x + 896 = 0.
Giải phương trình trên và loại nghiệm x = 32 (> 30) ta được x = 28cm.
Từ I hạ IE ⊥ Bx, trong tam giác IBE vuông tại E thì 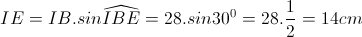(cũng có thế sử dụng kiến thức về nửa tam giác đều)
Câu hỏi liên quan
-
Thấu kính trên là thấu kính gì (HS tự giải)? Vẽ hình (HS tự giải) . Tính tiêu cự của thấu kính và độ lớn của các ảnh theo h; d1 và d2.
-
Thay nước bằng một chất lỏng khác, KLR của chất lỏng phải thế nào để thực hiện được việc trên?
-
Để cục nước đá chuyển hoàn toàn sang thể hơi ở 1000C thì cần một nhiệt lượng là bao nhiêu kJ? Cho nhiệt dung riêng của nước và nước đá là C1 = 4200J/kg.K; C2 = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.105 J/kg; nhiệt hóa hơi của nước là L = 2,3.106 j/kg.(Bỏ qua sự mất nhiệt với môi trường ngoài).
-
Pa-lăng ở câu trên được mắc theo cách khác nhưng vẫn có
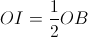(Hình 3) người đó phải tác dụng vào dây một lực F bằng bao nhiêu để tấm ván OB nằm ngang thăng bằng ? Tính lực F’ do ván tác dụng vào điểm tựa O ? (Bỏ qua ma sát ở các ròng rọc và trọng lượng của dây, của ròng rọc) -
Tính cường độ dòng điện trong mạch chính theo x, L, R1 và R2.
-
Hãy tính điện trở tương đương của đoạn mạch AB và số chỉ của ampe kế trong hai trường hợp : 1.Khóa K mở. 2.Khóa K đóng.
-
Một chùm sáng song song với trục chính tới thấu kính, phản xạ trên gương và cho ảnh là một điểm sáng S. Vẽ đường đi của các tia sáng (HS tự giải) và giải thích, tính khoảng cách SF’ .
-
Tính lượng nước m và nhiệt độ khi có cân bằng nhiệt trong bình 2 (t’2).
-
Tính giá trị toàn phần của biến trở và vị trí con chạy C.
-
Nếu bỏ cục nước đá trên vào ca nhôm đựng nước ở 200C thì khi có cân bằng nhiệt, người ta thấy có 50g nước đá còn sót lại chưa tan hết. Tính khối lượng nước đựng trong ca nhôm lúc đầu hết ca nhôm có khối lượng 100g và nhiệt dung riêng của nhôm là C3 = 880 J/kg.K. (Bỏ qua sự mất nhiệt với môi trường ngoài).