BF // AM

Câu hỏi
Nhận biếtBF // AM
A.
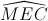 và
và 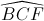 là hai góc đồng vị
là hai góc đồng vị
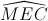 và
và 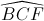 là hai góc đồng vị
là hai góc đồng vị
B.
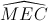 và
và 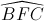 là hai góc đồng vị
là hai góc đồng vị
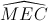 và
và 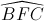 là hai góc đồng vị
là hai góc đồng vị
C.
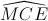 và
và 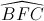 là hai góc đồng vị
là hai góc đồng vị
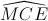 và
và 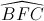 là hai góc đồng vị
là hai góc đồng vị
D.
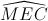 và
và 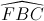 là hai góc đồng vị
là hai góc đồng vị
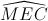 và
và 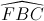 là hai góc đồng vị
là hai góc đồng vị Đáp án đúng: B
Lời giải của Luyện Tập 365
Ta có 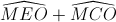 = 1800
= 1800
=>Tứ giác MEOC nội tiếp => 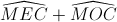
Mà 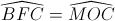 = (câu 3)
= (câu 3)
Do đó 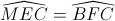
Ta có 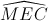 và
và 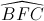 là hai góc đồng vị
là hai góc đồng vị
Vậy BF // AM
Ta có 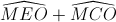 = 1800
= 1800
=>Tứ giác MEOC nội tiếp => 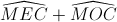
Mà 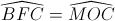 = (câu 3)
= (câu 3)
Do đó 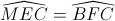
Ta có 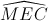 và
và 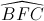 là hai góc đồng vị
là hai góc đồng vị
Vậy BF // AM
Câu hỏi liên quan
-

Giải hệ phương trình

-

Giải hệ phương trình với a = 2
-

Giải phương trình với a = -2
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Tính giá trị biểu thức của A với x =

-

Rút gọn A
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Tìm a để phương trình có 2 nghiệm nguyên
