Từ một tấm thiếc hình chữ nhật ABCD có chiều rộng AB = 3,6 dm, chiều dài AD = 4,85 dm, người ta cắt một phần tấm thiếc để làm mặt xung quanh của một hình nón với đỉnh là A và đường sinh bằng 3,6dm, sao cho diện tích mặt xung quanh này lớn nhất. Mặt đáy của hình nón được cắt trong phần còn lại của tấm thiếc hình chữ nhật ABCD. Trả lời câu hỏi dưới đây:Chứng tỏ rằng có thể cắt được nguyên ven hình nón đáy mà chỉ sử dụng phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón nói trên.

Câu hỏi
Nhận biếtTừ một tấm thiếc hình chữ nhật ABCD có chiều rộng AB = 3,6 dm, chiều dài AD = 4,85 dm, người ta cắt một phần tấm thiếc để làm mặt xung quanh của một hình nón với đỉnh là A và đường sinh bằng 3,6dm, sao cho diện tích mặt xung quanh này lớn nhất. Mặt đáy của hình nón được cắt trong phần còn lại của tấm thiếc hình chữ nhật ABCD.
Trả lời câu hỏi dưới đây:
Chứng tỏ rằng có thể cắt được nguyên ven hình nón đáy mà chỉ sử dụng phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón nói trên.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta chứng minh tồn tại một đường tròn có bán kính bằng 0,5dm nằm trong phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón, thật vậy:
Trên đường chéo AC, vẽ (I; 0,9 dm) như hình vẽ.
Gọi IH, IK lần lượt là các đoạn vuông góc kẻ từ I đến BC và CD.
Ta có CI = AC – AI = 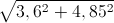 - (3,6 + 0,9) ≈ 1,54(dm)
- (3,6 + 0,9) ≈ 1,54(dm)
Vì IH //AB => 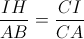 => IH =
=> IH = 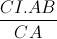 = 1,54.3,6.
= 1,54.3,6.
Ta chứng minh tồn tại một đường tròn có bán kính bằng 0,5dm nằm trong phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón, thật vậy:
Trên đường chéo AC, vẽ (I; 0,9 dm) như hình vẽ.
Gọi IH, IK lần lượt là các đoạn vuông góc kẻ từ I đến BC và CD.
Ta có CI = AC – AI = 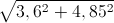 - (3,6 + 0,9) ≈ 1,54(dm)
- (3,6 + 0,9) ≈ 1,54(dm)
Vì IH //AB => 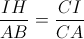 => IH =
=> IH = 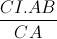 = 1,54.3,6.
= 1,54.3,6.
Câu hỏi liên quan
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Giải phương trình (1) khi m = -5
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Giải hệ phương trình với a = 2
-

Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
