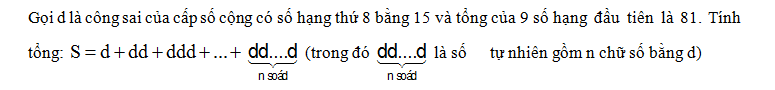Cho lăng trụ tam giác ABC.A’B’C’. Gọi M,N,P lần lượt là trung điểm các cạnh AB; AA’; A’C’. Thiết diện của lăng trụ khi cắt bởi (MNP) là hình gì?

Câu hỏi
Nhận biếtCho lăng trụ tam giác ABC.A’B’C’. Gọi M,N,P lần lượt là trung điểm các cạnh AB; AA’; A’C’. Thiết diện của lăng trụ khi cắt bởi (MNP) là hình gì?
Đáp án đúng: C
Lời giải của Luyện Tập 365


Câu hỏi liên quan
-

Giải các phương trình sau:
a)
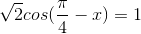
b)
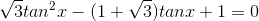
-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

-

Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?
-

-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-

-

: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-

Tìm số hạng không chứa x trong khai triển của nhị thức
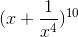
-