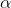Cho (H) là đồ thị của hàm số 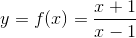 .
Hãy lựa chọn phép tịnh tiến song song với trục Ox để nhận được đồ thị hàm số
.
Hãy lựa chọn phép tịnh tiến song song với trục Ox để nhận được đồ thị hàm số 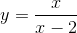 .
.

Câu hỏi
Nhận biếtCho (H) là đồ thị của hàm số 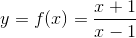 .
.
Hãy lựa chọn phép tịnh tiến song song với trục Ox để nhận được đồ thị hàm số 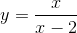 .
.
Đáp án đúng:
Lời giải của Luyện Tập 365
Ta có:
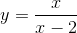
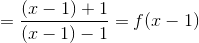 .
.
Vậy, đồ thị của hàm số được suy ra bằng phép tịnh tiến (H) theo Ox sang phải 1 đơn vị.
Ta có:
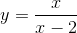
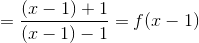 .
.
Vậy, đồ thị của hàm số được suy ra bằng phép tịnh tiến (H) theo Ox sang phải 1 đơn vị.
Câu hỏi liên quan
-

Cho góc
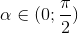 thỏa mãn
thỏa mãn 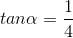 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của 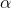
-

Dùng định nghĩa tính khoảng tăng giảm của hàm số:
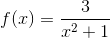
-

Cho a, b, c, d là các số thực dương. Chứng minh rằng:
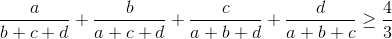
-

. Cho tam giác ABC với A(-1;2);B(-2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành
-

Cho a,b,c là số thực dương. Chứng minh rằng:
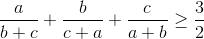
-

Dùng định nghĩa tìm khoảng tăng giảm của hàm số:
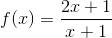
-

Tìm miền xác định của hàm số sau:

-

Phần nâng cao
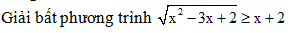

-

Phần cơ bản
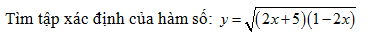

-

Cho góc
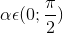 thỏa mãn
thỏa mãn 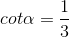 . Tính các giá trị lượng giác của
. Tính các giá trị lượng giác của