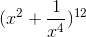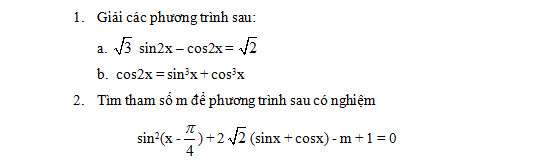Cho tứ diện ABCD với AB vuông góc với (BCD) và AB = a ; đáy BCD là tam giác đều ,cạnh 2a . Tính góc giữa 2 mặt phẳng ((ACD) và (BCD)

Câu hỏi
Nhận biếtCho tứ diện ABCD với AB vuông góc với (BCD) và AB = a ; đáy BCD là tam giác đều ,cạnh 2a . Tính góc giữa 2 mặt phẳng ((ACD) và (BCD)
Đáp án đúng:
Lời giải của Luyện Tập 365
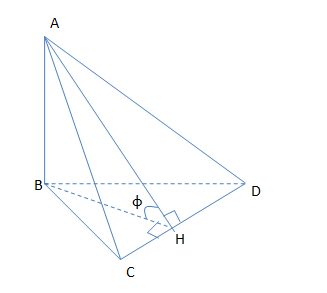
Đây là trường hợp đặc biệt :
Kẻ \(\left\{ \matrix{AB \bot \left( {BCD} \right) \hfill \cr AH \bot CD \hfill \cr} \right. \Rightarrow BH \bot CD \Rightarrow \angle AHB\) là góc giữa 2 mặt phẳng (ACD) và (BCD)
Trong tam giác ABH có :
\(\tan \varphi = {{AB} \over {BH}} = {a \over {2a{{\sqrt 3 } \over 2}}} = {{\sqrt 3 } \over 2} \Rightarrow \varphi = {30^0}\)

Đây là trường hợp đặc biệt :
Kẻ \(\left\{ \matrix{AB \bot \left( {BCD} \right) \hfill \cr AH \bot CD \hfill \cr} \right. \Rightarrow BH \bot CD \Rightarrow \angle AHB\) là góc giữa 2 mặt phẳng (ACD) và (BCD)
Trong tam giác ABH có :
\(\tan \varphi = {{AB} \over {BH}} = {a \over {2a{{\sqrt 3 } \over 2}}} = {{\sqrt 3 } \over 2} \Rightarrow \varphi = {30^0}\)
Câu hỏi liên quan
-

-

-

Tìm tập xác định của các hàm số sau:
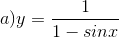
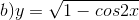
-

Tìm tập xác định của các hàm số sau:
a)
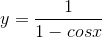
b)
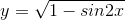
-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

-

-

-

-

Tìm số hạng không chứa x trong khai triển của nhị thức