Cho tứ diện ABCD . Chứng minh rằng điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là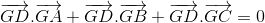 
Câu hỏi
Nhận biếtCho tứ diện ABCD . Chứng minh rằng điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là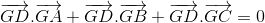
Đáp án đúng:
Lời giải của Luyện Tập 365
+) Thuận : Do G là trọng tâm của tam giác ABC nên ta có :
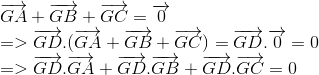
+) Đảo :
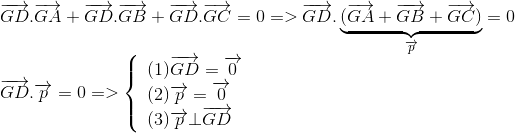
Khả năng (1) và (3) không xảy ra
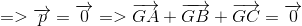
=>G là trọng tâm tam giác ABC
+) Thuận : Do G là trọng tâm của tam giác ABC nên ta có :
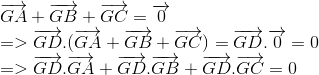
+) Đảo :
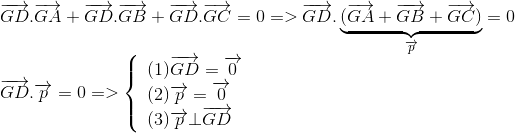
Khả năng (1) và (3) không xảy ra
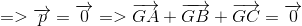
=>G là trọng tâm tam giác ABC
Câu hỏi liên quan
-
-
: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-
-
Tìm tập xác định của các hàm số sau:
-
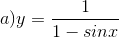
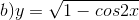
Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-
Cho
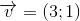và đường thẳng d: y=2x+2 Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
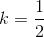và phép tịnh tiến theo vectơ . -
Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?
-
-
Một hộp kín chứa 2 quả cầu màu trắng và 8 quả cầu màu đen, các quả cầu chỉ khác nhau về màu sắc. Lấy ngẫu nhiên 3 quả từ hộp đã cho.
a) Tính xác suất để lấy được 3 quả cầu cùng màu.
b) Tính xác suất để lấy được ít nhất một quả cầu màu đen.
-
bai 5 de 2 hk1 minhkhai ha tinh 13 -14
