Cho hình chóp S.ABCD a) Nếu đáy ABCD là hình bình hành , chứng minh: \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) b) Nếu đáy ABCD là hìnhchữ nhật , chứng minh: \(S{B^2} + S{D^2} = S{A^2} + S{C^2}\)

Câu hỏi
Nhận biếtCho hình chóp S.ABCD
a) Nếu đáy ABCD là hình bình hành , chứng minh:
\(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \)
b) Nếu đáy ABCD là hìnhchữ nhật , chứng minh:
\(S{B^2} + S{D^2} = S{A^2} + S{C^2}\)
Đáp án đúng:
Lời giải của Luyện Tập 365
a)
Gọi I là tâm hình bình hành ABCD , theo qui tắc trung điểm ta có :
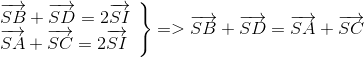
b) ABCD là hình chữ nhật , suy ra : IA = IB = IC = ID
Ta có :
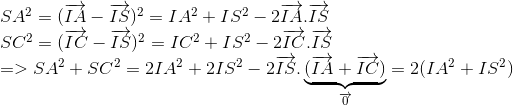
Tương tự :
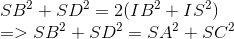
a)
Gọi I là tâm hình bình hành ABCD , theo qui tắc trung điểm ta có :
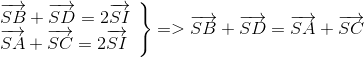
b) ABCD là hình chữ nhật , suy ra : IA = IB = IC = ID
Ta có :
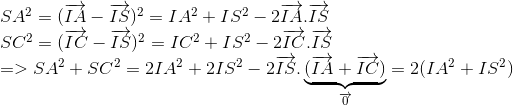
Tương tự :
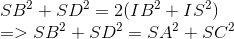
Câu hỏi liên quan
-

Tìm số hạng không chứa x trong khai triển của nhị thức
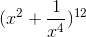
-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

-

-

bai 5 de 2 hk1 minhkhai ha tinh 13 -14

-

-

-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?