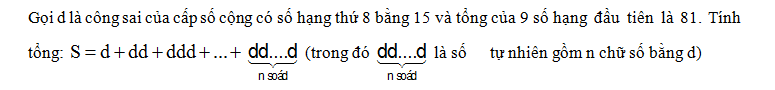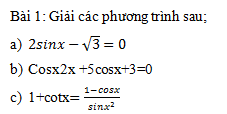Cho tứ diện ABCD . Gọi I ; J lần lượt là trung điểm các cạnh AB ; CD . Lấy điểm M  AD ; N
AD ; N  BC sao cho
BC sao cho 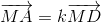 và
và 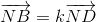 ( k ≠ 1) . Chứng minh 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.
( k ≠ 1) . Chứng minh 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.

Câu hỏi
Nhận biếtCho tứ diện ABCD . Gọi I ; J lần lượt là trung điểm các cạnh AB ; CD . Lấy điểm M 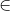 AD ; N
AD ; N 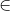 BC sao cho
BC sao cho 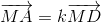 và
và 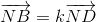 ( k ≠ 1) . Chứng minh 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.
( k ≠ 1) . Chứng minh 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.
Đáp án đúng:
Lời giải của Luyện Tập 365
Ta có :
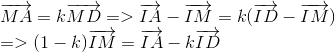
Chứng minh tương tự ta có : 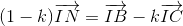
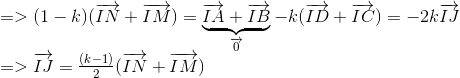
Suy ra 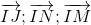 đồng phẳng
đồng phẳng
Vậy 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.
Ta có :
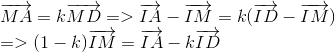
Chứng minh tương tự ta có : 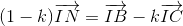
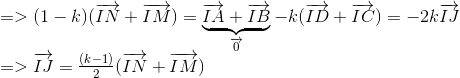
Suy ra 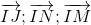 đồng phẳng
đồng phẳng
Vậy 4 điểm I ; J ; M ; N thuộc cùng 1 mặt phẳng.
Câu hỏi liên quan
-

-

Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?
-

-

-

Tìm số hạng không chứa x trong khai triển của nhị thức
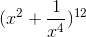
-

Một hộp kín chứa 2 quả cầu màu trắng và 8 quả màu đen, các quả cầu chỉ khác nhau về màu sắc.
a) Lấy ngẫu nhiên 3 quả cầu từ hộp đã cho. Tính xác suất để lấy được ba quả cầu cùng màu.
b) Lấy ngẫu nhiên các quả cầu từ hộp đã cho hai lần như sau: Lần thứ nhất lấy ra 3 quả cầu rồi trả lại vào hộp. Lần thứ 3 lấy ra 3 quả cầu. Tính xác suất để số cầu trắng của hai lần lấy là như nhau.
-

Tìm số hạng không chứa x trong khai triển của nhị thức
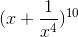
-

-

Cho
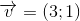 và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số
và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 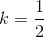 và phép tịnh tiến theo vecto
và phép tịnh tiến theo vecto 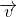 .
. -

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?