Cho hình chóp S.ABCD. Trên 3 cạnh SA ; SB ; SD lấy các điểm O ; G ; P tùy ý. a) Tìm thiết diện tạo nên do (GOP) và S.ABCD b) Chứng minh 2 giao tuyến ∆1 ; ∆2 của mặt phẳng (GOP) với 2 mặt phẳng (SBC và (SCD) cắt nhau tại 1 điểm nằm trên SC.
Câu hỏi
Nhận biếtCho hình chóp S.ABCD. Trên 3 cạnh SA ; SB ; SD lấy các điểm O ; G ; P tùy ý.
a) Tìm thiết diện tạo nên do (GOP) và S.ABCD
b) Chứng minh 2 giao tuyến ∆1 ; ∆2 của mặt phẳng (GOP) với 2 mặt phẳng (SBC và (SCD) cắt nhau tại 1 điểm nằm trên SC.
Đáp án đúng:
Lời giải của Luyện Tập 365
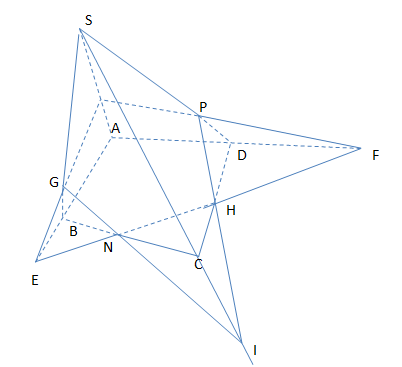
a)
Trong mặt phẳng (SAB) ta có :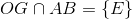
Trong mặt phẳng (SAD) ta có :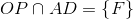
Trong mặt phẳng (ABCD) ta có :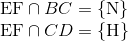
Vậy HNGOP là thiết diện cần tìm.
b) Gọi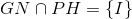 
Ta chứng minh :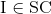 
. Thật vậy:
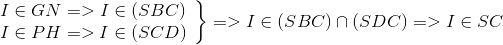
Điều phải chứng minh.
a)
Trong mặt phẳng (SAB) ta có :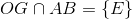
Trong mặt phẳng (SAD) ta có :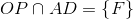
Trong mặt phẳng (ABCD) ta có :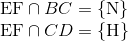
Vậy HNGOP là thiết diện cần tìm.
b) Gọi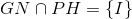
Ta chứng minh : 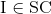. Thật vậy:
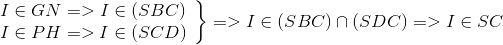
Điều phải chứng minh.
Câu hỏi liên quan
-
: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-
Gieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 7.
b) Các mặt xuất hiện có số chấm bằng nhau.
-
Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-
Giải các phương trình sau:
a)
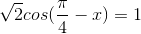
b)
-
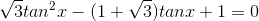
Tìm số hạng không chứa x trong khai triển của nhị thức
-
-
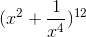
Cho
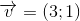và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
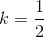và phép tịnh tiến theo vecto 
. -
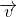Giải các phương trình sau:
a)
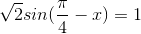
b)
-
-
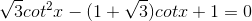
