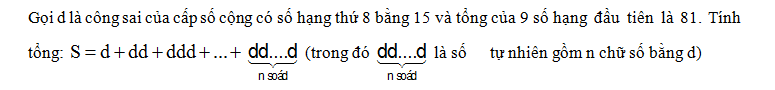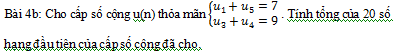Cho M ; N ; P là 3 điểm tùy ý trên các cạnh SA ; SC ; BC của tứ diện SABC. a) Tìm giao điểm Q của (MNP) với cạnh AB b) Chứng minh QM ; SB , PN đồng qui

Câu hỏi
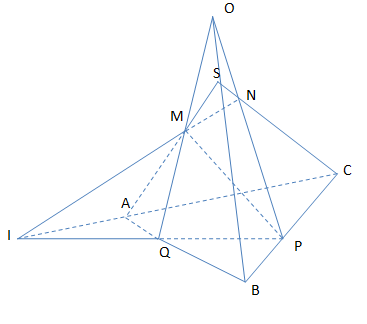
Nhận biếtCho M ; N ; P là 3 điểm tùy ý trên các cạnh SA ; SC ; BC của tứ diện SABC.
a) Tìm giao điểm Q của (MNP) với cạnh AB
b) Chứng minh QM ; SB , PN đồng qui
Đáp án đúng:
Lời giải của Luyện Tập 365
a) Trong mặt phẳng (SAC) ta có : 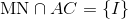
Trong mặt phẳng (ABC) ta có : 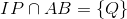
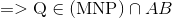
b) Trong mặt phẳng (INP) ta có: 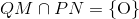
Do 3 điểm S ; B ; O thuộc giao tuyến của 2 mặt phẳng (AQM) và (CPN) nên S ;B ; O thẳng hàng
=> Điều phải chứng minh

a) Trong mặt phẳng (SAC) ta có : 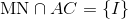
Trong mặt phẳng (ABC) ta có : 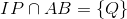
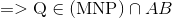
b) Trong mặt phẳng (INP) ta có: 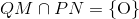
Do 3 điểm S ; B ; O thuộc giao tuyến của 2 mặt phẳng (AQM) và (CPN) nên S ;B ; O thẳng hàng
=> Điều phải chứng minh
Câu hỏi liên quan
-

bai 5 de 2 hk1 minhkhai ha tinh 13 -14

-

-

Giải các phương trình sau:
a)
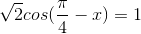
b)
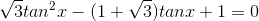
-

-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-

-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-