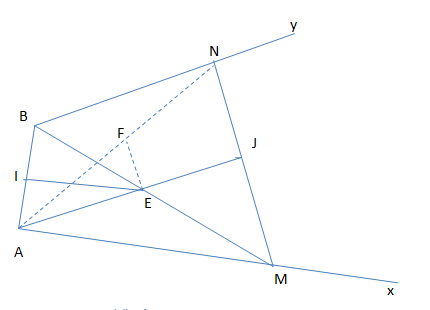
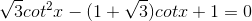Trong không gian cho 2 tia Ax và By chéo nhau. Trên Ax lấy điểm M , trên By lấy điểm N . Gọi I và J lần lượt là trung điểm của AB và MN và E là trung điểm của BM. Tìm giao điểm 2 mặt phẳng: a) (IMN) và (JAB) b) (EIJ) và (ABN) ; (EIJ) và (AMN)

Câu hỏi
Nhận biếtTrong không gian cho 2 tia Ax và By chéo nhau. Trên Ax lấy điểm M , trên By lấy điểm N . Gọi I và J lần lượt là trung điểm của AB và MN và E là trung điểm của BM. Tìm giao điểm 2 mặt phẳng:
a) (IMN) và (JAB)
b) (EIJ) và (ABN) ; (EIJ) và (AMN)
Đáp án đúng:
Lời giải của Luyện Tập 365
a) 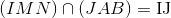
b) Gọi F là trung điểm của AN
Ta có : FJ // AM
EI // AM
=>EI // FJ => 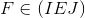
Vậy :
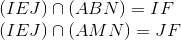

a) 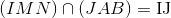
b) Gọi F là trung điểm của AN
Ta có : FJ // AM
EI // AM
=>EI // FJ => 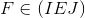
Vậy :
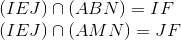
Câu hỏi liên quan
-

-

-

bai 5 de 2 hk1 minhkhai ha tinh 13 -14

-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-

-

-

Tìm tập xác định của các hàm số sau:
a)
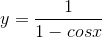
b)
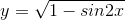
-

Giải các phương trình sau:
a)
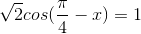
b)
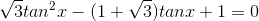
-

-

Giải các phương trình sau:
a)
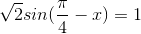
b)