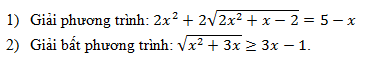Giải các phương trình :
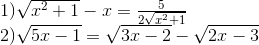

Câu hỏi
Nhận biếtGiải các phương trình :
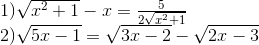
2)x = 2
2)x = 2
2)x = 1/6
2)x = 1/6
Đáp án đúng: A
Lời giải của Luyện Tập 365
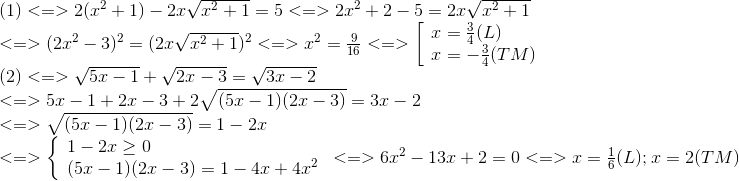
Câu hỏi liên quan
-

Tìm tập xác định của hàm số sau;
a)
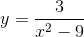
b)
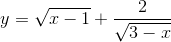
c)
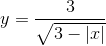
-

Dùng định nghĩa tính khoảng tăng giảm của hàm số:
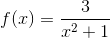
-

BAN CƠ BẢN

-

Cho a,b,c là số thực dương. Chứng minh rằng:
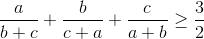
-

Cho a, b, c, d là các số thực dương. Chứng minh rằng:
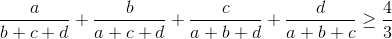
-

Phần nâng cao

-

Cho góc
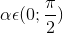 thỏa mãn
thỏa mãn 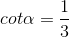 . Tính các giá trị lượng giác của
. Tính các giá trị lượng giác của 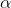
-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
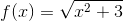
-

-

Xác định hàm số bậc hai
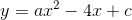 biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1).
biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1).