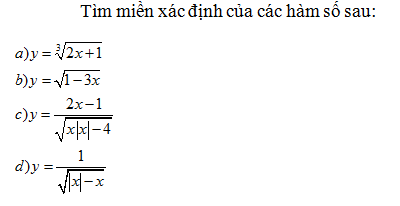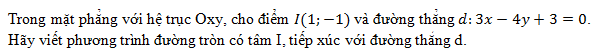Giải hệ phương trình :
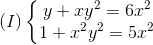

Câu hỏi
Nhận biếtGiải hệ phương trình :
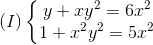
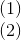
A.
(1;2)
B.
(1;2) ; ( ½ ; 1)
C.
(1;-2) ; ( -½ ; 1)
D.
(-1;2) ; ( ½ ; 1)
Đáp án đúng: B
Lời giải của Luyện Tập 365
Từ (2) => x ≠ 0 => y ≠ 0 ( do (1) )
Chia 2 phương trình cho x2 ≠ 0
=12](https://luyentap365.com/wp-content/picture/learning/exam/2015/0905/v99559_577562_1.gif)
Đặt 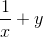 = t . Ta có :
= t . Ta có :
t3 – 5t – 12 = 0 < => (t – 3)( t2 + 3t + 4) = 0 < => t = 3
Vậy 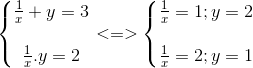
Vậy hệ có nghiệm (1;2) ; ( ½ ; 1)
Từ (2) => x ≠ 0 => y ≠ 0 ( do (1) )
Chia 2 phương trình cho x2 ≠ 0
=12](https://luyentap365.com/wp-content/picture/learning/exam/2015/0905/v99559_577562_1.gif)
Đặt 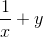 = t . Ta có :
= t . Ta có :
t3 – 5t – 12 = 0 < => (t – 3)( t2 + 3t + 4) = 0 < => t = 3
Vậy 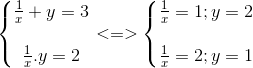
Vậy hệ có nghiệm (1;2) ; ( ½ ; 1)
Câu hỏi liên quan
-

-

Tìm miền xác định của hàm số sau:

-

Cho góc
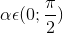 thỏa mãn
thỏa mãn 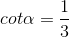 . Tính các giá trị lượng giác của
. Tính các giá trị lượng giác của 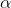
-

Dùng định nghĩa để tìm khảng tăng giảm của hàm số
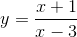
-

Giải và biện luận phương trình sau theo tham số m
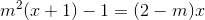
-

Phần nâng cao
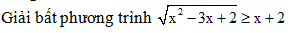

-

BAN NÂNG CAO

-

-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
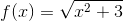
-

. Cho tam giác ABC với A(-1;2);B(-2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành