Giải hệ phương trình :
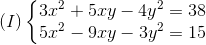
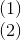

Câu hỏi
Nhận biếtGiải hệ phương trình :
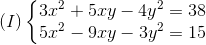
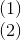
A.
(3;1) và (-3;-1)
B.
(-3;1) và (3;-1)
C.
(3;1) và (1;3)
D.
(3;1) và (3;-1)
Đáp án đúng: A
Lời giải của Luyện Tập 365
+) Với x = 0 thì thay vào (1) cho vô nghiệm.
+) Đặt y = tx thế vào hệ ta có :
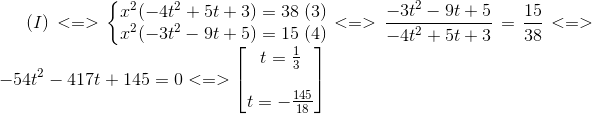
* Với t = 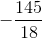 ta có :
ta có : 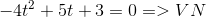
* Với t = 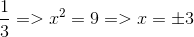
Vậy hệ có 2 nghiệm (3;1) và (-3;-1)
+) Với x = 0 thì thay vào (1) cho vô nghiệm.
+) Đặt y = tx thế vào hệ ta có :
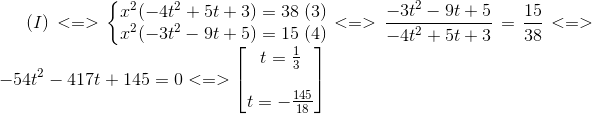
* Với t = 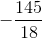 ta có :
ta có : 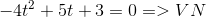
* Với t = 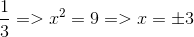
Vậy hệ có 2 nghiệm (3;1) và (-3;-1)
Câu hỏi liên quan
-

Phần cơ bản
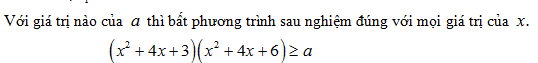
-

Cho a,b,c là số thực dương. Chứng minh rằng:
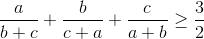
-

-

Cho góc
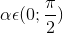 thỏa mãn
thỏa mãn 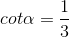 . Tính các giá trị lượng giác của
. Tính các giá trị lượng giác của 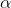
-

-

Xác định hàm số bậc hai
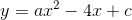 biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1).
biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1). -

-

-

Xác định hàm số bậc hai
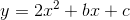 biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2)
biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2) -

cơ bản