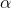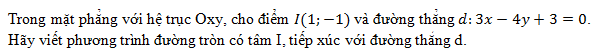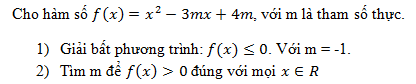Giải các phương trình sau :
1) 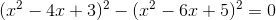 2)
2) 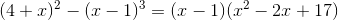

Câu hỏi
Nhận biếtGiải các phương trình sau :
1) 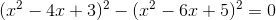
2) 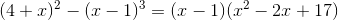
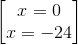
2)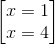
2) x = -24
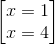
2)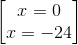
2) x = 0
Đáp án đúng: C
Lời giải của Luyện Tập 365
1)
![(x^{2}-4x+3)^{2}-(x^{2}-6x+5)^{2}=0 <=> \left [(x^{2}-4x+3) + (x^{2}-6x+5 \right ].\left [ (x^{2}-4x+3) - (x^{2}-6x+5)\right ]=0 <=>(2x-2)(2x^{2}-10x+8)=0](https://luyentap365.com/wp-content/picture/learning/exam/2015/0901/v99374_91742_1.gif)
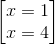
2) 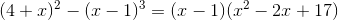
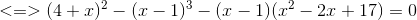
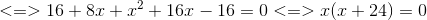
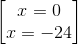
1)
![(x^{2}-4x+3)^{2}-(x^{2}-6x+5)^{2}=0 <=> \left [(x^{2}-4x+3) + (x^{2}-6x+5 \right ].\left [ (x^{2}-4x+3) - (x^{2}-6x+5)\right ]=0 <=>(2x-2)(2x^{2}-10x+8)=0](https://luyentap365.com/wp-content/picture/learning/exam/2015/0901/v99374_91742_1.gif)
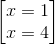
2) 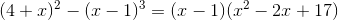
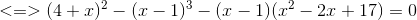
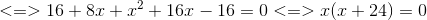
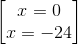
Câu hỏi liên quan
-

Xác định hàm số bậc hai
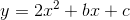 biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2)
biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2) -

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
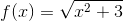
-

Tìm tập xác định của hàm số sau;
a)
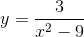
b)
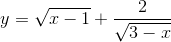
c)
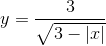
-

-

-

Giải và biện luận phương trình sau theo tham số m
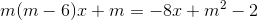
-

Xác định hàm số bậc hai
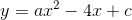 biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1).
biết rằng đồ thị của nó cắt Oy tại điểm có tung độ -3 và đi qua điểm M(-2;1). -

BAN NÂNG CAO
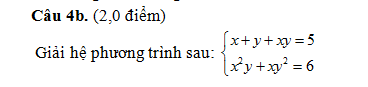
-

cơ bản

-

Cho góc
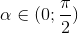 thỏa mãn
thỏa mãn 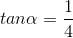 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của