∆MNQ là tam giác đều.

Câu hỏi
Nhận biết∆MNQ là tam giác đều.
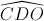 =
= 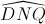 ; DC = QD
; DC = QD 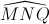 = 600.
= 600. 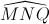 = 600.
= 600. Đáp án đúng: B
Lời giải của Luyện Tập 365
Vì 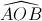 = 600 (gt) =>
= 600 (gt) => 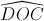 = 600
= 600
=> 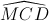 +
+ 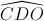 = 600 (4)
= 600 (4)
Mặt khác 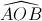 = 600 =>
= 600 => 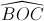 = 600.
= 600.
ABCD là hình thang cân => OB = OC.
Suy ra ∆BOC là tam giác đều có CN là trung tuyến thì NQ =  DC = QD hay ∆NQD cân tại Q
DC = QD hay ∆NQD cân tại Q
=> 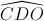 =
= 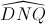 (5)
(5)
Thay (3), (5) vào (4) ta được: 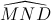 +
+ 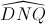 = 600 hay
= 600 hay 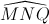 = 600 (6)
= 600 (6)
Chứng minh tương tự ta được MQ là trung tuyến của tam giác vuông DMC
=> MQ = NQ =  CD (7)
CD (7)
Từ (6) và (7) => ∆MNQ là tam giác đều.
Vì 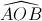 = 600 (gt) =>
= 600 (gt) => 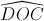 = 600
= 600
=> 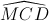 +
+ 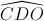 = 600 (4)
= 600 (4)
Mặt khác 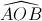 = 600 =>
= 600 => 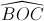 = 600.
= 600.
ABCD là hình thang cân => OB = OC.
Suy ra ∆BOC là tam giác đều có CN là trung tuyến thì NQ =  DC = QD hay ∆NQD cân tại Q
DC = QD hay ∆NQD cân tại Q
=> 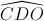 =
= 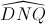 (5)
(5)
Thay (3), (5) vào (4) ta được: 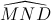 +
+ 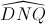 = 600 hay
= 600 hay 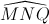 = 600 (6)
= 600 (6)
Chứng minh tương tự ta được MQ là trung tuyến của tam giác vuông DMC
=> MQ = NQ =  CD (7)
CD (7)
Từ (6) và (7) => ∆MNQ là tam giác đều.
Câu hỏi liên quan
-

Tính giá trị biểu thức của A với x =

-

Giải hệ phương trình với a = 2
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Tìm b để A =

-

Chứng minh rằng: AM2 = AN.AB
-

Giải phương trình (1) khi m = -5
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
